에라토스테네스의 체

최근 알고리즘 문제를 풀고 있는데, 소수를 찾는 문제를 자주 접한다.

물론 BruteForce 방식으로 찾아도 기능상엔 문제가 없지만, 수행 속도면에서 몇몇 문제의 결과가 실패로 나타나곤 한다.

이때 에라토스테네스의 체라는 개념을 접하게 되었다.

 

에라토스테네스의 체란?

에라토스테네스의 체는 무엇일까?

고대 그리스 수학자가 체로 숫자를 걸러내는 방식이라 하여 체라는 단어가 붙었다고 한다. 이는 소수를 찾기 위한 가장 간단하고 빠른 방법으로 알려져있다.

방법

1부터 100까지 숫자가 있다고 가정하자.

소수도 아니고 합성수도 아닌 자연수 1을 제외하자.

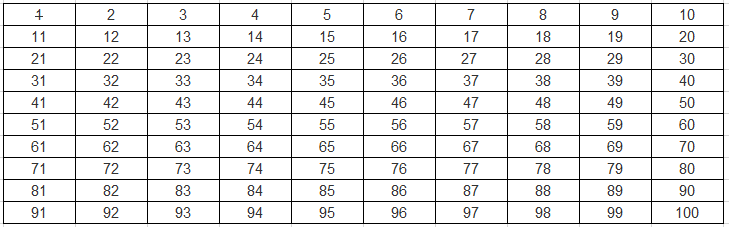
2를 제외한 모든 2의 배수는 소수가 아니니 제외하자.

3을 제외한 모든 3의 배수는 소수가 아니니 제외하자.

4의 배수는 2의 배수를 처리할 때 이미 지워졌으니 넘어가고 5를 제외한 5의 배수를 제외하자.

6의 배수는 3의 배수를 처리할 때 이미 지워졌으니 넘어가고 7을 제외한 7의 배수를 제외하자.

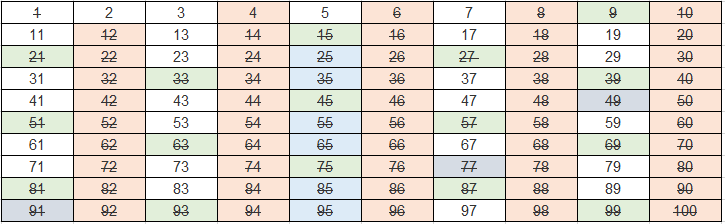
8, 9, 10의 배수는 이미 앞선 2, 3, 5의 배수에서 지워졌으니 넘어간다. 11이상의 수의 경우는 배수가 100을 넘어가니 더 이상 확인하지 않는다.

 

구현

GitHub - jaywapp/Jaywapp.Algorithm

public static List<int> Calculate(int n)
{
    var arr = new bool[n + 1];

	// 탐색 시작
    for(int i = 2; i <= n; i++)
    {
        if (!arr[i])
        {
            var next = i + i;
            // 배수 체크
            for (int j = next; j <= n; j += i)
                arr[j] = true;
        }
    }

    var result = new List<int>();

    for(int i = 2; i<= n; i++)
    {
    	// 체크되지 않은 항목 반환
        if (!arr[i])
            result.Add(i);
    }

    return result;
}